Lecciones
Fracciones equivalentes
Publicado por admin el 26/10/2016. Ubicación de la lección en el curriculum: FRACCIONES, 5PRIM, FRACCIONES0.Objetivo de la lección
- Concepto de fracción equivalente
- Distinguir cuándo dos fracciones son equivalentes
- Calcular fracciones equivalentes
1.Introducción, lo que ya sé…
Fracciones más grandes que la unidad
…Ya conozco que existen fracciones mayores que la unidad. Son todas aquellas en las que el numerador es mayor que el denominador…
Por ejemplo: ${5/3}$ , ${5/4}$ , ${8/2}$
Fracciones equivalentes a un número natural
…Ya conozco que hay fracciones que son equivalentes a números naturales. Son todas aquellas que al dividir entre sí numerador y denominador, me dan como resto 0. Por ejemplo: ${8/2}$ , ${20/4}$ , ${100/10}$
2.Fracciones equivalentes
En el siguiente gráfico, hemos dividido un círculo de iguales dimensiones de 3 maneras distintas:
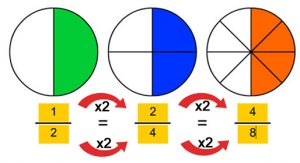
En el primer caso lo hemos partido en 2 mitades; en el segundo caso en cuatro y en el tercer caso en 8 partes iguales. En todos los casos hemos coloreado la mitad del círculo. Sin embargo, la manera de expresar la mitad del círculo es distinta en cada caso:
En el primer círculo, la mitad coloreada queda expresada como ${1/2}$
En el segundo círculo, la mitad coloreada queda expresada como ${2/4}$
Y en el tercer círculo, la mitad coloreada queda expresada como ${4/8}$
Las 3 expresiones representan la misma mitad del círculo, y son por ello equivalentes.
Decimos que las tres fracciones son equivalentes y podemos escribir:
Decimos que las tres fracciones son equivalentes y podemos escribir:
${1/2}$ = ${2/4}$ = ${4/8}$
Distinguir fracciones equivalentes
2 fracciones son equivalentes si coinciden los productos cruzados de numeradores y denominadores. Ejemplo:
${4/5}$ y ${12/15}$ son FRACCIONES EQUIVALENTES, ya que: 4 x 15 = 5 x 12
Generar fracciones equivalentes a partir de una dada
Para generar fracciones equivalentes a partir de una fracción dada, basta con multiplicar o dividir numerador y denominador por el mismo número.
Vamos a generar un par de fracciones equivalentes a ${20/25}$
Vamos a generar un par de fracciones equivalentes a ${20/25}$
En el primer caso, dividimos numerador y denominador entre 5:
${( 20 : 5 )/(25 : 5)}$ = ${4/5}$
En el segundo, multiplicamos numerador y denominador por 3:
${ ( 20 x 3 )/(25 x 3)}$ = ${60/75}$



