Lecciones
Qué es una fracción. Partes de la unidad
Publicado por admin el 31/10/2016. Ubicación de la lección en el curriculum: FRACCIONES, 5PRIM, FRACCIONES0.Objetivo de la lección
- Entender una fracción como una forma de nombrar una parte de la unidad
- Leer fracciones con denominador mayor que 10
- Pensar la fracción más allá del concepto explicado en esta lección
1…lo que ya sé…
Términos de una fracción: Numerador y denominador
…En cursos anteriores, aprendiste a nombrar los dos términos de una fracción:
la parte situada por encima de la línea horizontal se le llama «numerador»
y la parte situada por debajo es el «denominador».
Así, sabes que en la fracción ${2/3}$ ,
el 2 es el «numerador»
y el 3, el «denominador»
Lectura de fracciones con denominador hasta 10
…En cursos anteriores, aprendiste también a leer fracciones con denominador inferior al número 11: Para leer la fracción primero nombrábamos el numerador como tal número ( por ejemplo, si tenemos un 4, leemos «cuatro» ) y a continuación expresábamos el denominador de la siguiente manera:
Si aparecía un 1, leíamos «enteros».
Cuando teníamos un 2, leíamos «medios», ya que en medias partes dividimos la unidad cuando se divide entre 2.
Si un 3, leíamos «tercios», ya que en tercios queda dividida la unidad cuando la dividimos en tres partes,… El resto de denominadores se leen así:
Un 4 en el denominador, se lee como «cuartos».
El 5 en el denominador, se lee como «quintos».
Cuando un 6, se lee como «sextos».
Un 7, como «séptimos»; un 8, como «octavos»; un 9, como «novenos» y finalmente, un 10 en el denominador, se lee como «décimos».
2.Situaciones
En la vida real, hacemos referencia con frecuencia a expresiones que representan el concepto matemático de fracción que estudiamos:
«Aproximadamente, ${7/10}$ partes de la superficie de la Tierra están cubiertas por agua»
![]()
«Sólo quiero la mitad del refresco»
«Más de ${4/5}$ de los alumnos de clase aprobaron el examen con buena nota»
El uso de este tipo de expresiones resulta muy apropiado cuando se trata de hacer visualizar a qué parte del todo de un objeto o de una propiedad del objeto, afecta una determinada circunstancia de la que hablamos. Observa el distinto impacto que produce la primera expresión frente a la expresión alternativa » 361.132.000 km${^2}$ de la superficie de la Tierra están cubiertos por agua». Ambas expresan una misma cualidad sobre la superficie de la Tierra, pero con efecto muy distinto.
3.Entender una fracción como una forma de nombrar una parte de una unidad

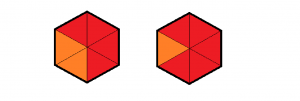
Las partes del hexágono que hemos pintado de color rojo son 2, pero no basta con decir esto para precisar su tamaño, como verás:
Las partes del hexágono que hemos pintado de color rojo son también 2, como en el primer caso, pero su tamaño difiere notablemente.
En el primer caso diremos que las partes en rojo son » 2 de un total de 6″ y en el segundo » 2 de 3″, que en notación matemática, escribiremos respectivamente como «${2/6}$» y «${2/3}$»
3. Lectura de fracciones con denominador a partir de 10
Cuando en el denominador tenemos números mayores que 10, la lectura del denominador se hace añadiendo al número que tengamos en el denominador el sufijo «avo». ( En caso de que el número del denominador termine en a, se suprime esta última letra para evitar la «cacofonía» ). La lectura del numerador se sigue haciendo como hasta ahora.
Así la fracción ${15/40}$, se lee como » quince cuarentavos«
4. Ultima nota para nota
La siguiente figura muestra la fracción ${9/6}$, que son las partes pintadas en rojo: