Lecciones
Comparación de fracciones con mismo numerador o mismo denominador
Publicado por admin el 27/10/2016. Ubicación de la lección en el curriculum: FRACCIONES, 5PRIM, FRACCIONES0.Objetivo de la lección
- Poner en contexto el sentido de comparar 2 fracciones entre sí
- Aprender a comparar fracciones, aplicando el concepto de fracción como partes de la unidad
- Aprender a comparar fracciones, aplicando el concepto de fracción como división entre 2 números
- Aprender a aplicar reglas rápidas para los casos de comparación de fracciones con mismo numerador o mismo denominador
1…lo que ya sé…
¿Qué es una fracción?
…En cursos anteriores, aprendiste el concepto de fracción, como el número de partes iguales que se toman de una unidad que ha sido dividida en un número de partes iguales. La fracción ${2/3}$ nos indica que nos referimos a 2 de las partes, de un total de 3 en las que la unidad ha sido dividida
Términos de una fracción: Numerador y denominador
…En cursos anteriores, aprendiste a nombrar los dos términos de una fracción:
la parte situada por encima de la línea horizontal se le llama «numerador»
y la parte situada por debajo es el «denominador».
Así, sabes que en la fracción ${2/3}$ ,
el 2 es el «numerador»
y el 3, el «denominador»
En esta lección, pretendemos comparar varias fracciones entre sí y poder ordenarlas. Queremos hacerlo comprensible utilizando los conceptos de fracción que hemos visto en este curso: fracción entendida como parte de la unidad y fracción entendida como división entre 2 números naturales.
2.Introducción
¿Para qué sirve comparar varias fracciones?
Estamos acostumbrados a distinguir entre dos números naturales distintos, como el 1 y el 2, y dado que son distintos, decir cuál de ellos es mayor o menor. La misma curiosidad nos mueve a distinguir entre 2 fracciones, y visto que son distintas, poder decir cuál de ellas es mayor o menor.
¿ Prefieres un tercio o la mitad de mi pastel ?
Estamos acostumbrados a distinguir entre dos números naturales distintos, como el 1 y el 2, y dado que son distintos, decir cuál de ellos es mayor o menor. La misma curiosidad nos mueve a distinguir entre 2 fracciones, y visto que son distintas, poder decir cuál de ellas es mayor o menor.
¿ Prefieres un tercio o la mitad de mi pastel ?

3. Comparación de fracciones, vistas como partes de la unidad
Observa las siguientes figuras. En ambas, mostramos el mismo hexágono dividido en 6 partes iguales:

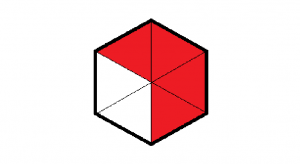
En la primera hemos pintado de rojo 2 de las 6 partes y en la segunda, 4. La primera figura representa gráficamente la fracción ${2/6}$ y la segunda, la fracción ${4/6}$. Será mayor la fracción que representa mayor superficie coloreada. En este caso, se observa que ${4/6}$ es mayor que ${2/6}$, que escribimos como ${4/6}$ > ${2/6}$. Observa que al comparar dos fracciones con el mismo denominador, será mayor la fracción que tenga el numerador mayor.
Observa ahora las siguientes 2 figuras: El mismo hexágono lo hemos dividido en 3 y en 6 partes iguales, y en ambos casos hemos coloreado 2 partes:
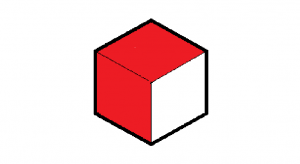

La primera figura representa gráficamente la fracción ${2/3}$ y la segunda, la fracción ${2/6}$. Como en el caso anterior, será mayor la fracción que represente mayor superficie coloreada. En este caso, observamos que ${2/3}$ es mayor que ${2/6}$, que escribimos como ${2/3}$ > ${2/6}$. Observa que al comparar 2 fracciones que tienen el mismo numerador, será mayor la fracción que tenga el denominador menor.
Observa finalmente las siguientes 2 figuras: El mismo hexágono lo hemos dividido en 3 y en 6 partes iguales; en el primer caso hemos coloreado 2 partes y en el segundo 5:


La primera figura representa gráficamente la fracción ${2/3}$ y la segunda, la fracción ${5/6}$. Como en los anteriores casos, será mayor la fracción que representa mayor superficie coloreada. En este caso, observamos que ${5/6}$ es mayor que ${2/3}$, que escribimos como ${5/6}$ > ${2/3}$
4. Comparación de fracciones, vistas como división entre 2 números
Si en cursos pasados aprendiste a dividir dos números entre sí sacando decimales y a comparar dos números decimales, te será fácil ahora comparar dos fracciones que se te presenten. Basta que entiendas que una fracción se puede interpretar como la división entre dos números y por tanto, para compararlas, efectuaremos las divisiones y compararemos los números decimales que surjan como resultado.
Imagina que queremos comparar las fracciones ${2/3}$ y ${5/6}$ del caso anterior. Para la primera fracción, ${2/3}$, si dividimos 2 entre 3, obtenemos 0,66. En el caso de la segunda fracción, ${5/6}$, si dividimos 5 entre 6, obtenemos 0,83. Por comparación de ambos números decimales, podemos decir que 0,83 es mayor que 0,66 y lo mismo podremos decir de las fracciones de las que los obtuvimos: ${5/6}$ es mayor que ${2/3}$
Imagina que queremos comparar las fracciones ${2/3}$ y ${5/6}$ del caso anterior. Para la primera fracción, ${2/3}$, si dividimos 2 entre 3, obtenemos 0,66. En el caso de la segunda fracción, ${5/6}$, si dividimos 5 entre 6, obtenemos 0,83. Por comparación de ambos números decimales, podemos decir que 0,83 es mayor que 0,66 y lo mismo podremos decir de las fracciones de las que los obtuvimos: ${5/6}$ es mayor que ${2/3}$



