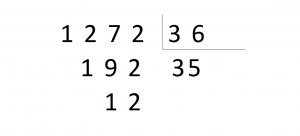Lecciones
Operaciones con números naturales
Publicado por admin el 30/07/2016. Ubicación de la lección en el curriculum: Números naturales, 5PRIM, Números naturales0.Objetivo de la lección
- Multiplicación de números naturales de 3 cifras
- Propiedad distributiva de la multiplicación respecto de la suma
- Operaciones combinadas
- División por un número de hasta 3 cifras
- Cambios en los términos de una división
1.Introducción
Conocemos de cursos anteriores las operaciones básicas de la suma, la resta, el producto y la división de números naturales.También conocemos algunas de sus propiedades que podremos aplicar cuando lo necesitemos:
Propiedad conmutativa de la suma de dos números naturales
4 + 2 = 2 + 4
Esta propiedad nos dice que obtenemos el mismo resultado al sumarle 2 a 4 que al sumarle 4 a 2
Propiedad asociativa de la suma de varios números naturales
Esta propiedad nos indica que cuando sumemos varios números naturales, el orden en que hagamos las sumas no afectará al resultado.¿ Cómo nos ayuda esta propiedad ?
Imagina la operación: 7 + 9 + 1. Si seguimos el orden de operación que se nos presenta sumaremos primero 7 + 9 y al resultado le sumaremos 1. O sea, que para calcular, haremos 7 + 9 + 1 = ( 7 + 9 ) + 1. Pero según la propiedad asociativa, nada nos impide hacer:
7 + 9 + 1 = 7 + ( 9 + 1 ) En este caso haremos primero la operación 9 + 1 y a su resultado le sumaremos 7.
Quizás esta segunda forma nos resulta más sencilla que la primera por la facilidad de obtener 9 + 1 frente a 9 + 7.
La propiedad asociativa nos dice que en ambos casos, el resultado obtenido será el mismo
Propiedad conmutativa del producto de dos números naturales
Propiedad asociativa del producto de varios números naturales
5 x 3 x 7 = ( 5 x 3 ) x 7 = 5 x ( 3 x 7 )
¿ Cómo nos ayuda esta propiedad ?
Imagina la operación: 7 x 5 x 2. Si seguimos el orden de operación que se nos presenta multiplicaremos primero 7 x 5 y el resultado lo multiplicaremos por 2. O sea, que para calcular, haremos 7 x 5 x 2 = ( 7 x 5 ) x 2. Pero según la propiedad asociativa, nada nos impide hacer:
7 x 5 x 2 = 7 x ( 5 x 2 ) En este caso haremos primero la operación 5 x 2 y a su resultado lo multiplicaremos por 7.
Quizás esta segunda forma nos resulta más sencilla por la facilidad de obtener primero 5 x 2 = 10 y luego multiplicar 7 x 10, frente a la primera opción.
La propiedad asociativa nos dice que en ambos casos, el resultado obtenido será el mismo
2.Multiplicación de números de 3 cifras entre sí
Procedimiento
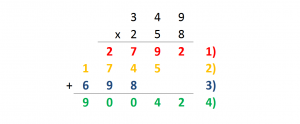
1) En primer lugar multiplicamos 349 x 8 y anotamos el resultado 2792 en la primera fila. Muy importante: Observa que el 2 de las unidades de 2792 se escribe justo debajo del 8 y que los siguientes números a su izquierda ocupan las posiciones consecutivas.
2) A continuación multiplicamos 349 x 5 y anotamos el resultado 1745 en la segunda fila. Muy importante: Observa que el 5 de las unidades de 1745 se escribe justo debajo del 5 y que los siguientes números a su izquierda ocupan las posiciones consecutivas.
3) En la tercera fila escribimos el resultado de 349 x 2, 698. Observa que el 8 de las unidades de 698 se escribe justo debajo del 2 y que los siguientes números a su izquierda ocupan las posiciones consecutivas.
4) Finalmente sumamos las filas 1, 2 y 3 y obtenemos el resultado de la multiplicación: 90.042
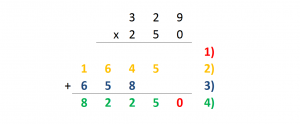
Caso particular de un número que acaba en 0
3.Propiedad distributiva de la multiplicación ( respecto de la suma o la resta )
La propiedad distributiva, nos dice que:
Vamos a intentar demostrarlo:
Imagina que no conocemos la propiedad distributiva y procedemos con el cálculo 3 x ( 5 + 8 ):En virtud de la propiedad conmutativa del producto de 2 números podemos escribir:
3 x ( 5 + 8 ) = ( 5 + 8 ) x 3 y a continuación, operamos los términos dentro del paréntesis: ( 5 + 8 ) x 3 = 13 x 3 = 39
Veamos si aplicando la propiedad distributiva llegamos al mismo resultado:
3 x ( 5 + 8 ) = 3 x 5 + 3 x 8 = 15 + 24 = 39
¡¡ EL MISMO RESULTADO¡¡
Pruébalo tú, cambiando los números
¿ Cómo nos ayuda esta propiedad ?
¿ Cuándo se nos presenta esta operación ?
» Tres amigos van a la tienda a comprar bolígrafos. Cada uno de ellos compra dos bolis azules, uno rojo y uno negro. ¿ cuántos bolis han comprado entre todos ellos ?»
4.Operaciones combinadas

En Matemáticas se establecen convenios o reglas que hacen que todos comprendamos lo mismo. Es como una especie de código de la circulación para evitar accidentes. En el caso de varias operaciones encadenadas como las mostradas, rigen las siguientes reglas de operación:
- En primer lugar se efectúan las operaciones que están dentro de los paréntesis
- En segundo lugar, las operaciones de multiplicación y división en el orden en que aparezcan
- En tercer y último lugar, las sumas y las restas en el orden en que aparezcan
Vamos ahora a practicar las reglas con los 4 ejemplos.
CASO 1: 3-2+1
Una vez eliminados los paréntesis en el paso anterior, procedemos con las multiplicaciones y las divisiones en el orden en que nos aparezcan: No hay multiplicaciones ni divisiones, así que no hacemos nada.
El tercer paso nos dice que sumemos y restemos en el orden en que aparezcan las operaciones:
La primera operación que aparece es 3-2, operamos y escribimos su resultado y el resto de operaciones que nos queden: 1 + 1
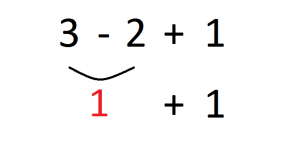
Seguimos operando, en este caso con la última operación 1 + 1 = 2, que es el resultado:
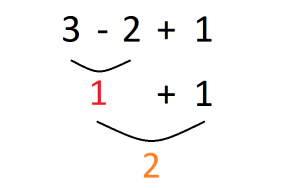
CASO 2: 3 -( 2+1 )
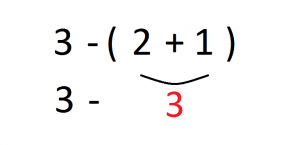
Una vez eliminados los paréntesis en el paso anterior, procedemos con las multiplicaciones y las divisiones en el orden en que nos aparezcan: No hay multiplicaciones ni divisiones, así que no hacemos nada.
En el tercer paso sumamos y restamos en el orden en que aparezcan las operaciones:
La primera y única operación que nos queda es 3 -3, operamos y escribimos su resultado, 0:
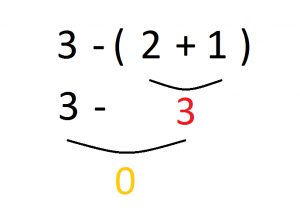
CASO 3: 5 + 2 x 3 – 2
Una vez eliminados los paréntesis en el paso anterior, procedemos con las multiplicaciones y las divisiones en el orden en que nos aparezcan. Vemos que nos aparece la multiplicación 2 x 3, escribimos su resultado y el resto de la expresión pendiente de operar:
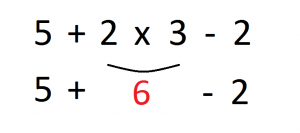
En el tercer paso sumamos y restamos en el orden en que aparezcan las operaciones:
La primera operación que aparece es 5 + 6 = 11, escribimos el resultado y el resto de la expresión pendiente de operar:
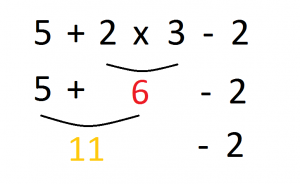
La segunda y última operación que aparece es 11-2, operamos y escribimos el resultado final, 9:
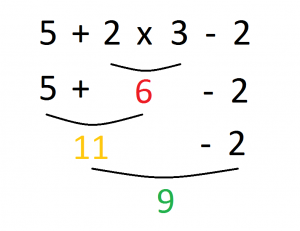
CASO 4: 5 + 2 x ( 3 – 2 )
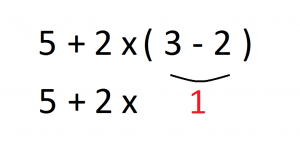
Una vez eliminados los paréntesis en el paso anterior, procedemos con las multiplicaciones y las divisiones en el orden en que nos aparezcan. Vemos que nos aparece la multiplicación 2 x 1, escribimos su resultado y el resto de la expresión pendiente de operar:
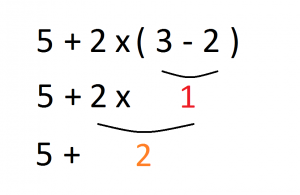
En el tercer paso sumamos y restamos en el orden en que aparezcan las operaciones:
La primera y última operación que aparece es 5 + 2, operamos y escribimos el resultado final, 7:
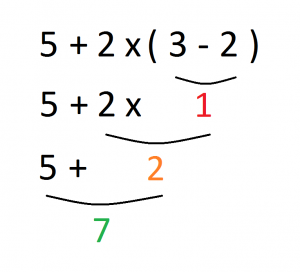
5.División por un número de hasta 3 cifras
División con divisor de 2 cifras
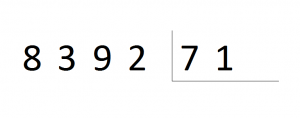
Pruebo el 2: 71 x 2 = 142 > 83, me paso.
Pruebo el 1: 71 x 1 = 71 < 83, me vale y la diferencia es 83 – 71 = 12. Escribo pues:
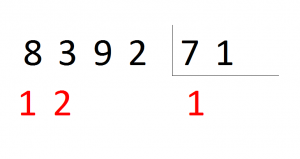
Pruebo el 2: 71 x 2 = 142 > 129, me paso.
Pruebo el 1: 71 x 1 = 71 < 129, me vale, y la diferencia es 129 – 71 = 58. Escribo pues:

Pruebo el 9: 71 x 9 = 639 > 582, me paso.
Pruebo el 8: 71 x 8 = 568 < 582, me vale y la diferencia es 582 – 568 = 14. Escribo pues:

La división está terminada.Comprueba la relación que se establece entre los términos de la división:
División con divisor de 3 cifras

6.Cambios en los términos de una división