Lecciones
Sistema de numeración romano
Publicado por admin el 23/08/2016. Ubicación de la lección en el curriculum: Sistemas de numeración, 5PRIM, Sistemas de numeración0.Objetivo de la lección
- Proponer sistemas de numeración alternativos al sistema decimal
- Fundamentar la comprensión de los sistemas
- Exponer las reglas de formación de números en el sistema romano
1.Introducción
Tipos de sistemas de numeración
Por semejanza con el comportamiento de los niños, que utilizan los dedos para contar, los antropólogos afirman que el sistema de numeración decimal es consustancial al ser humano, al estar basado en el número de dedos de las dos manos. El sistema de numeración en base 10 fue utilizado por los griegos, pero no representaban los dígitos con la grafía conocida hoy en día por nosotros ( el 2, por ejemplo, se escribía β’) y no hacían uso del dígito 0.El origen de la grafía de los números actuales lo encontramos en la India. Dicho sistema fue conocido y adoptado por los matemáticos musulmanes del actual Irak y fueron los árabes quiénes en su expansión territorial durante los siglos VIII al XV, lo introdujeron en Europa, donde pasó a ser de uso extendido a partir del siglo XIV.
Así pues, el sistema de numeración decimal, se impuso sobre otros que coexistieron en el tiempo, como por ejemplo el sistema de numeración romano y que será objeto de un estudio somero en esta lección.
El sistema de numeración romano está basado a su vez en el sistema etrusco. A grandes rasgos, la principal diferencia entre los sistemas etrusco-romano y decimal es que mientras el segundo se basa en la posición que ocupa cada dígito para establecer el valor del total del número, los primeros se basan en un sistema aditivo ( al que luego se añadió una regla sustractiva para evitar la extensión ) que consiste en establecer el valor total del número como adición de los dígitos que lo componen.
Veamos un ejemplo inventado para los dos tipos de sistemas:
Un sistema de numeración POSICIONAL, el «debasetres»
Como ejemplo de un sistema de numeración POSICIONAL, hemos ideado un sistema alternativo al decimal al que llamaremos «debasetres», que a diferencia del sistema decimal que conocemos, que establece su base sobre 10 ( es decir, 10 unidades forman una decena, que es el orden siguiente al de las unidades, 10 decenas forman una centena, que es el orden siguiente al de las decenas, etc…), establecerá su base sobre el número 3.Así como en el sistema decimal necesitamos 10 dígitos, en nuestro sistema «debasetres» necesitaremos sólo 3 , que responderán a la misma grafía que los tres primeros dígitos del sistema decimal: 0, 1 y 2. ( podríamos también representarlos con otros símbolos distintos ideados por nosotros ). Con estos 3 dígitos, organizaremos todo nuestro sistema «debasetres».
Además, aplicaremos nuevas reglas de formación de unidades posicionales, basadas en el 3, en lugar del 10: En el primer nivel con el 0, el 1 y el 2 representaremos las unidades de nuestro sistema, con las que sólo podremos expresar hasta 2 unidades; en el siguiente nivel, 3 unidades formarán un «trío» ( en lugar de una decena ) y podremos expresar hasta ocho unidades ( 8=3X3-1 ). La última unidad que puedo representar en cada nivel sale de restar uno al 3 multiplicado tantas veces por sí mismo como el número de nivel en el que me encuentro. En el siguiente nivel 3 tríos formarán un «noneto» y podremos expresar hasta 26 unidades ( 3 X 3 x 3 -1 ), y así sucesivamente… Nuestros números en «debasetres» tendrán el siguiente aspecto:
| Unidades representadas | Representación simbólica en «debasetres» |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 10 |
| 4 | 11 |
| 5 | 12 |
| 6 | 20 |
| 7 | 21 |
| 8 | 22 |
| 9 | 100 |
| 10 | 101 |
| 11 | 102 |
| 12 | 110 |
| 13 | 111 |
| 14 | 112 |
| 15 | 120 |
| 16 | 121 |
| 17 | 122 |
| 18 | 200 |
| 19 | 201 |
| 20 | 202 |
| 21 | 210 |
| 22 | 211 |
| 23 | 212 |
| 24 | 220 |
| 25 | 221 |
| 26 | 222 |
| 27 | 1000 |
| etc… | etc… |
Resulta extraño ver llamar a 27 unidades «1.000», pero así es en nuestro sistema «debasetres». Observa en la siguiente figura el número de unidades que representa nuestro «121» en «debasetres»:
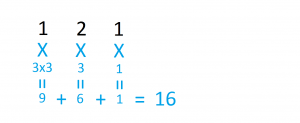
También curiosa resulta la suma de números en nuestro sistema: Como puedes observar en la siguiente figura, en el sistema decimal expresamos la suma de 11 y 14 unidades como se muestra a la izquierda; en nuestro sistema, 11 unidades se expresan como 102 y 14, como 112, y la suma queda:
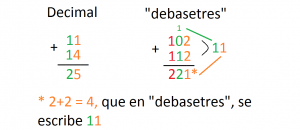
Un sistema de numeración ADITIVO, el «etrumano»
Aquí va un ejemplo de un SISTEMA de numeración ADITIVO, que nos hemos inventado: Se trata del «etrumano» y contiene un único símbolo, llamado «etruno», que equivale a la unidad y que se representa como:![]()
Si en nuestro particular sistema de numeración queremos representar 3 unidades, escribiremos:

Como puedes ver, uno de los inconvenientes que tiene nuestro sistema «etrumano» es que cuando queremos escribir números grandes tenemos que escribir muchos símbolos y además, resultará muy complicado leerlos.
Para paliar parcialmente este inconveniente introducimos en nuestro «sistema etrumano», un nuevo símbolo, al que llamamos «decatrumano» y que equivale a 10 unidades y cuyo símbolo es:

Ahora, para representar 30 unidades, nos hemos ahorrado pintar uno detrás de otro, 30 «etrunos» y lo hacemos de esta forma con ayuda de los nuevos «decatrumanos»:

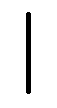
2. El sistema de numeración romano
Mejor que seguir ideando nuestro «etrumano», veremos ahora un par de fundamentos de un sistema de numeración aditivo consolidado y trabajado durante siglos, como el sistema romano y cuyos vestigios todavía a día de hoy se reconocen en la nomenclatura de los siglos o en algunos relojes.
Los dígitos del sistema romano
Así como el sistema decimal utiliza los dígitos 0,1,2…hasta el 9, el sistema romano utiliza sus propios símbolos para representar los dígitos:
I equivale a la unidad, 1
V, equivale a 5 unidades
X, 10 unidades
L, 50
C, 100
D, 500
y M, 1.000
Regla de la adición para la composición de números en el sistema romano
Como otros sistemas aditivos, el sistema romano compone sus números mediante la adición del valor de los dígitos que componen la cadena. Por ejemplo:
MDCCXII representa 1.712 unidades ya que M+D+C+C+X+I+I son ( 1.000+500+100+100+10+1+1 ) 1.712 unidades
Regla de la resta para la composición de números en el sistema romano
Para evitarse cadenas de números largas y de lectura compleja, los romanos idearon la regla de la resta que consiste en hacer que los dígitos I, X y C, colocados a la izquierda de los dos dígitos de más valor siguientes a cada uno de ellos, restan su valor. Así, por ejemplo:
XL y XC, representan el 40 ( 50-10 ) y el 90 ( 100-10 ), pero no se escribe XD para escribir 400
Finalmente, CD y CM representan el 400 ( 500-100 ) y el 900 ( 100-100 )
Regla de repetición permitida
Regla de la multiplicación por mil
Para el 4.000 y siguientes, deberíamos escribir MMMM. Sin embargo, la regla anterior nos prohíbe el uso de más de 3 dígitos M. La regla de la multiplicación por mil nos dice que una raya horizontal sobre un dígito o grupo de dígitos, multiplica el valor del dígito o del grupo por mil. Así, para expresar 4.000, utilizamos IV



