Lecciones
Suma y Resta de dos o más fracciones con el mismo denominador
Publicado por admin el 29/10/2016. Ubicación de la lección en el curriculum: FRACCIONES, 5PRIM, FRACCIONES0.Objetivo de la lección
- Identificar situaciones reales en las que se presente la cuestión
- Fundamentar la comprensión
- Facilitar un método de cálculo
1.Introducción
Cuando manejamos fracciones, como cuando manejamos números naturales, surgen situaciones en las que se precisa operar con ellas. Las operaciones entre fracciones que veremos en esta lección son la SUMA y la RESTA. El concepto de suma y resta de fracciones es equivalente al de la suma y resta de números naturales y se aplica en situaciones similares.
2.Suma de fracciones y suma de números
 Para resolver el problema, planteamos la SUMA de las ciruelas comidas por uno y otro Así concluimos que entre ambos comieron 2+3 = 5 ciruelas. Plantearemos una cuestión similar en el ámbito de las fracciones:»Juan comió ${1/5}$ de pizza y Marta, ${2/5}$, ¿cuánta/s pizza/s comieron entre ambos?»Como en el caso anterior, la cuestión responde al concepto de suma. Se resuelve también sumando en este caso las fracciones de pizza comidas por cada uno de ellos. Y así podemos escribir que entre ambos comieron: ${1/5}$ + ${2/5}$. Veremos más adelante, cómo resolver esta operación.
Para resolver el problema, planteamos la SUMA de las ciruelas comidas por uno y otro Así concluimos que entre ambos comieron 2+3 = 5 ciruelas. Plantearemos una cuestión similar en el ámbito de las fracciones:»Juan comió ${1/5}$ de pizza y Marta, ${2/5}$, ¿cuánta/s pizza/s comieron entre ambos?»Como en el caso anterior, la cuestión responde al concepto de suma. Se resuelve también sumando en este caso las fracciones de pizza comidas por cada uno de ellos. Y así podemos escribir que entre ambos comieron: ${1/5}$ + ${2/5}$. Veremos más adelante, cómo resolver esta operación.
3.Resta de fracciones y resta de números
Observa, ahora el caso de la RESTA:
«En el almacén de la tienda había 5 sillas. Ahora quedan 3. ¿ cuántas sillas salieron del almacén?»
Nuevamente en el ámbito de manejo de números naturales, necesitamos plantear una operación, que en este caso es la resta. Para dar con la cuestión restamos al número de sillas iniciales, las que quedan al final y podemos concluir que el número de sillas que salieron del almacén son 5-3=2 sillas.

Planteamos un caso equivalente en el ámbito de manejo de fracciones:
«Marta había realizado hasta ayer ${1/3}$ del trabajo. Al final de la tarde de hoy, lleva realizados ${2/3}$ ( !! ánimo, Marta ). ¿ cuánto trabajo ha realizado Marta durante el día de hoy?»
Como en el caso de los números naturales, el esquema mental que nos lleva a resolver el problema es similar: Buscaremos la diferencia entre el trabajo realizado al final del día de hoy y al principio: ${2/3}$ – ${1/3}$. Veremos también más adelante, cómo resolver esta operación.
4.Suma y Resta de fracciones con el mismo denominador
Nos limitaremos en esta lección a los métodos de SUMA y RESTA de fracciones con el mismo denominador, dejando para cursos superiores la SUMA y RESTA de fracciones con distinto denominador.
Para poder SUMAR o RESTAR dos o más fracciones, deberemos comprobar antes que las fracciones sean COHERENTES entre sí. Por COHERENCIA nos referimos a:
- En primer lugar, de la misma manera que en los números naturales, cada fracción de la suma debe hacer referencia al mismo tipo de objeto. Así, SI es posible sumar o restar 2 fracciones de pizza, de trabajo, de manzana, etc…Pero NO es posible sumar o restar una fracción de pizza y una de manzana, como no era posible hacerlo tampoco en el ámbito de los números naturales, propiedad que ya conoces.
- En el ámbito de las fracciones, la COHERENCIA entre fracciones a sumar o restar va un poco más allá que en el caso de los números naturales: afecta al hecho de que las fracciones en juego deben hacer referencia a la misma unidad de medida. Nos explicamos con un ejemplo:
La unidad de medida común es que ambas fracciones proceden de haber dividido la unidad en 6 partes. Una vez hecha la división en 6 partes, el primer término, ${4/6}$, hace referencia a 4 de las 6 partes y el 2º término, ${1/6}$, hace referencia a 1 de las 6 partes en que la unidad fue dividida. Es posible proceder con las operaciones de SUMA y RESTA pues ambas fracciones representan unidades de ${1/6}$: 4 unidades para el caso del primer término y 2 unidades para el segundo.Gráficamente, podemos «encajar» la fracción ${1/6}$ en la fracción ${4/6}$ en la suma y en la resta:
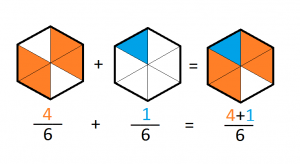
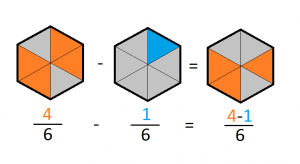
5.Procedimiento
Para sumar o restar dos fracciones:
- 1.Comprobamos la coherencia entre las fracciones: El denominador debe ser el mismo.
- 2.Sumamos o restamos sus numeradores y conservamos el denominador, que era común.



